ちょっとした話なんですが、嬉しいことがあったので自慢させてください。
長女次女、9歳。4月から小学4年生になる、ゲーム好き・漫画好き・お絵かき好きの双子です。
長女次女が小さいころから、一緒に「内緒見つけゲーム」をやっていました。お風呂に入っている間とか、ちょっと空いた時間に、「内緒」を一つ見つける。内緒を探し出した人は褒められる、というゲームです。
いや、内緒ってなんやねんという話なんですが、要は何かしらの図や表を見ていると見つかる、ぱっと見では分かりにくい法則のことなんです。
例えば、しんざき家のお風呂場には、こんなシートが貼ってあります。

何の変哲もない、ちょっとファンシーな九九の表ですね。
お風呂場の壁に貼れるように、水気で吸着するタイプのやつです。
もちろん九九なので、1×1から9×9までの掛け算が載っているのは当然なのですが、「実はこの表には、他にも色々内緒の秘密があります」とある時言ったんです。
その例として、「5の段は、右側の数字が0か5しかないです」ということを教えました。
「他の内緒も見つけてみよう!」と言ってみると、長女も次女も、お風呂に入りながら一生懸命「内緒」を探し始めました。
例えば「6の段の右の数字は、全部2の段の答えの数字しかない」
「4の段や8の段もそうだけど数字の並びが違う」とか、
「9の段の右の数字が、987654321と1ずつ減っている」とか、
「おっきな数字の色が赤・青・黄色と分かれている」とか
「数字が小さい段の生き物程大きい」とか
「蛇の舌の長さが皆おんなじ」とか、そういうのですね。
まあ、算数と関係あるものもあれば、何の関係もないものもあるんですが。
この時私が作ったルールって一個だけで、「それがどんな内緒であっても絶対に発見者を褒めるし、数学的な理由は一切説明しない」ということでした。
何かを見出して褒められるのは、もちろん発見のモチベーションになります。
その内緒の発見者は飽くまで長女次女であって欲しかったですし、細かい理由を説明して「もうパパは知ってる」ということをアピールしたくもなかった。
理論については、後から学校で習った時に、「あ、これ昔気付いたアレだ!!!」って感動を味わってもらえればそれが一番いいと思ったんです。進研ゼミでやったヤツだメソッドです。
これ、別に九九の表に限らなくって、他にもABCの表とか、あいうえお表とか、電車の路線図(電車好きの長男が持ってたヤツです)とか、世界地図とか、色々な図表でやりました。
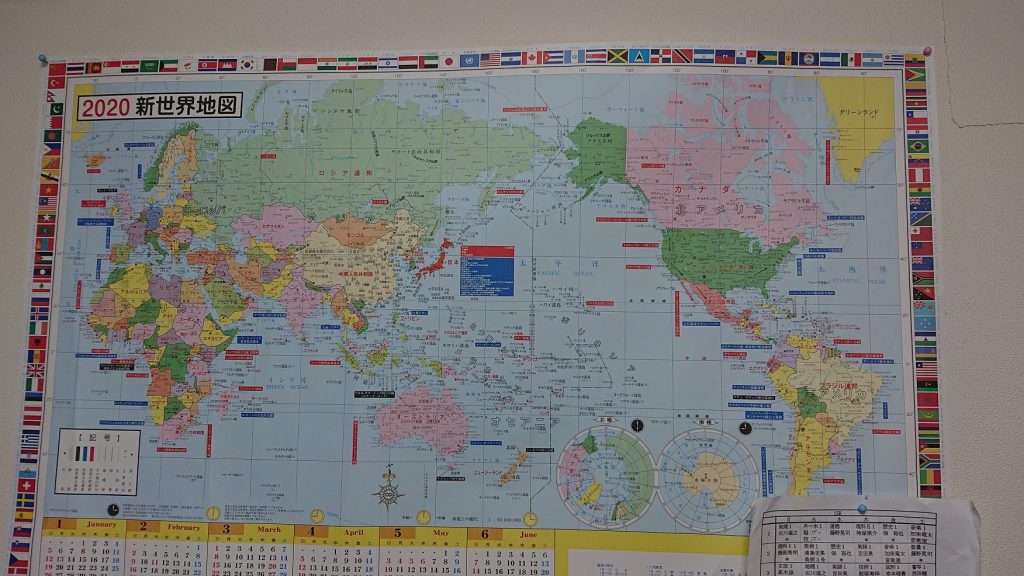
世界地図では、「この国(ポルトガル)から海だけを通ってこの国(日本)に行きたいです!どうやって行けばいいでしょうか!!」とか大航海時代ごっこをやっていたら、「ここ飛び越えたい」とか言ってあっさりスエズを突破されまして、期せずしてスエズ運河の重要性を説明出来たりしました。
ただまあ、もちろん私が誘導しつつなので、まだ自発的に何かを発見するには至りませんで、その場のノリで気付いたことを喋っている、という感じではありました。
もちろんそれだけでも十分だとは思うんですが。
一緒にお風呂に入らなくなって、この「内緒見つけゲーム」もその内あんまりやらなくなったんですが、先日長女と次女が二人でお風呂に入った後、次女がこんなことを言いました。
「ねえパパ、凄い内緒見つけちゃったかも」
暫く内緒見つけゲームをしていなかったので、最初何のことか分かりませんでした。
「え?内緒って?」
「九九の表見てて気付いたんだけど」
「はい」
「6×6って36だよね。7×5って35だよね?」
「うん」
「5×5が25で、6×4が24」
「うんうん」
「前と後ろの数は足すと一緒なのに、かけると全部1小さくなる……!!!!!」
取り敢えず私は、
「せ、世紀の大発見なのでは……!?」
と言っておきました。次女はとても嬉しそうに、胸を反らしてきゃっきゃ笑っていました。
私、実はこの時、ものすごーーく嬉しくなりまして。
これ、もちろん数学的に考えれば(x+1)*(x-1)=x~2-1という話なんですが、気付いたから偉い偉くないって話じゃなくって、「数列から一般的な法則を見つけ出す」という、いわば数学の源泉みたいなことに、誰に誘導されたわけでもなく、自分自身でたどり着いたことがすごーーく偉いと思ったんですよ。
そもそも「内緒探し」の動機として、何より「一見ばらばらな何かから、法則を発見する楽しさ」というのを味わってみて欲しかったんですよね。
一般性に落とし込む楽しさ。自分が法則を見出す快感。これって、多分人生のあらゆる場面で有用になってくる考え方だと思うんですよ。
ある法則を見つけ出す。それで他の事象についても説明出来る。これ、言ってみればアカデミズムの源泉です。
一般化の楽しさを知っていると、何より「見て、取り敢えず考える」という習慣が身に付きます。
ただの図表が、実は色々な内緒を隠していることを知っていると、「内緒を探そう」という視点で図表を見ることが出来ます。
図表の要素と要素がどう関係しているのか。そこには何か法則があるのかどうか。つまり、「データの意味」を最初に考えることが出来る。
更に、「一つの法則が、それ以外にも当てはまるのかどうか」という検証の思考も身につくんじゃないかなあ、と。
6×6と7×5は1違う。じゃあ他の数字ではどうだろう?それは全部の数字に当てはまるんだろうか?これって多分、エビデンスを元にした議論とか、科学的思考の萌芽でもあると思うんですよ。
そういった、いわば「思考の歩み」の種を蒔けていたとしたら、それはすごーく嬉しいことだなあと。
もちろん子どもの成長は非線形ですし、一度出来るようになったことが翌日には出来ないことが子どもにとってはデフォルトなので、これだけのことで何かが出来るようになった、とは間違っても言えません。明日には忘れている可能性は非常に高いです。
ただ、こういった「何かの考えのトリガー」を積み重ねることで、いつか何か大事なものが、長女や次女や、もちろん長男の頭の中でも芽吹くといいなあ、と。
そんな風に考えているわけなんです。
ちなみに、「内緒見つけゲーム」自体については、慣れてくると電車の中での暇つぶしとか、子どもたちを数分静かにさせておきたい時の時間稼ぎにも使えたりしますので、小学生の親御さんには結構お勧めです。
今日書きたいことはそれくらいです。
単なる理論ではなく、現場で成果を出す生成AI活用の“実装方法”を知りたい方に最適なウェビナーです。
本セミナーでは、製薬・バイオ企業でのPoC(概念検証)から得られた実データとノウハウを元に、「どこにAIが効くのか」「どこが難しいのか」を明確に解説します。

【開催概要】
・開催日:2026年2月12日(木)
・時間:12:00〜13:00
・形式:オンライン(Zoom/ログイン不要)
・参加費:無料(定員150名)
製薬・バイオ企業の生成AI導入は、「試行」から「実利」を問うフェーズへと移行しています。
本セミナーでは、13チームのPoCで時間を50〜80%削減したノウハウを余すことなく共有します。適用可否の見極め、評価設計、失敗領域への対応方法、全社展開のガバナンス設計まで、実践的な内容です。:contentReference[oaicite:1]{index=1}
・製薬・バイオ・化学業界のDX/業務改革担当者
・AI導入プロジェクト責任者・企画部門・法務・人事などの全社展開担当者
・PoC設計や効果測定の「型」を学びたい方
・自社の生成AI活用を確実な成果につなげたい実務担当者
【セミナーの内容】
・生成AIの“適用可否”を短期間で見切る方法(PoC設計・評価の型)
・現場で成果を出すAI活用ノウハウ(バックキャスティング/プロンプト構造化 等)
・適用が難しい領域(PowerPoint・OCR 等)の整理と次の打ち手への転換
・横展開に向けたガバナンス設計とナレッジ共有
【登壇者】
奥田 真輔 氏
システム開発やITコンサルティングを経て、
外資系製薬企業で15年以上のITビジネスパートナーとして人事からコマーシャル、 メディカルなど製薬企業の様々な分野のプロジェクトに携わる。
現在はネクセラファーマ株式会社で、システムだけではなく、企業風土改革や業務改善をリードし、
日本発グローバルバイオ製薬企業にむけて、同社の成長基盤の構築に尽力している。
岡田 雄太(ワークワンダース株式会社 CTO)
野村総合研究所に新卒入社後、証券総合バックオフィスシステムやオンライントレードシステムなどの開発に従事。
その後、8 Securities(現SoFi Hong Kong)へ出向し、日本人唯一のエンジニアとして国際的なプロジェクトに携わる。
BOOSTRYでは信託銀行向けSaaSの立ち上げと成長を牽引。
WiseVineではCTOとして開発組織を30名規模に拡大し、プロダクト開発を推進。
2025年4月よりワークワンダース株式会社CTOに就任。AI活用を中心とした開発支援をリードする。
【お申込み・詳細】
こちらのウェビナー申込ページをご覧ください。
(2026/01/19更新)
【著者プロフィール】
著者名:しんざき
SE、ケーナ奏者、キャベツ太郎ソムリエ。三児の父。
レトロゲームブログ「不倒城」を2004年に開設。以下、レトロゲーム、漫画、駄菓子、育児、ダライアス外伝などについて書き綴る日々を送る。好きな敵ボスはシャコ。
ブログ:不倒城
Photo:erokism
Photo :Kentaro Ohno









